Población UNAM

Sitio:	Tu Aula Virtual
Curso:	Matemáticas IV ENP - Ejemplo PAPIME
Libro:	Población UNAM

Impreso por:	Invitado
Fecha:	viernes, 13 de febrero de 2026, 15:00

Descripción

Tabla de Contenidos

1. Población UNAM

1. Población UNAM

Situación 6. Población UNAM

Instrucciones: Lee cuidadosamente toda la situación y pasa a la siguiente página.

La siguiente información se encuentra disponible en el Portal de Estadística Universitaria de la UNAM:

1. Realiza un gráfico de barras que muestre el porcentaje de incremento o decremento en el reingreso en estudiantes de bachillerato con respecto al ciclo escolar anterior.

2. Si

$n$ es la población escolar total y

$m$ es el porcentaje de mujeres, ¿cuál expresión puedes utilizar para determinar el número de estudiantes hombres en un ciclo escolar determinado?

3. En el ciclo escolar 1999-2000 ingresaron 32,530 alumnos, mientras que en el ciclo escolar 2019-2020 ingresaron 35,041 alumnos al bachillerato UNAM. Suponiendo que se tuviera un comportamiento lineal y creciente, modelado por la función

$f(p)=125.55p+32530$ , donde

$p$ es el tiempo en años transcurridos desde el ciclo escolar 1999-2000, ¿cuántos alumnos se atenderían durante el ciclo escolar 2029-2030?

4. En el ciclo escolar de 2018 a 2019, egresaron 29 335 estudiantes en total. Si al triple de alumnos que egresaron de la ENP se le resta el doble de alumnos que egresaron del CCH, se tiene 9 820 alumnos, ¿cuántos alumnos egresaron de la ENP en dicho ciclo?

5. El siguiente gráfico muestra la distribución de alumnos de nuevo ingreso por salón de clases en uno de los planteles de la ENP:

$x$ representa el número de hombres y

$y$ el número de mujeres por salón de clases, indica una inecuación que modele el problema.

1.1. Parte 1. Representación de información numérica en forma gráfica.

Objetivo

El estudiante:

Utilizará los contenidos de representación de información numérica en forma gráfica para resolver problemas contextualizados.

Productos esperados

Solución a un problema

Recursos

Guía de estudios de Matemáticas IV
Videos de YouTube

Actividad de aprendizaje

Materiales

Forma de trabajo: Individual

Indicaciones

1. Lee cuidadosamente y contesta las preguntas planteadas a partir de tus conocimientos y los recursos de apoyo que se te proporcionan.

Realiza un gráfico de barras que muestre el porcentaje de incremento o decremento en el reingreso en estudiantes de bachillerato con respecto al ciclo escolar anterior. Toma como referente, los datos de la siguiente tabla:

Nota: Para ver mejor la tabla, da clic sobre la imagen

Para dar solución al problema revisa los siguientes materiales:

Presta atención en lo siguiente:

Concepto de razones y proporciones
Porcentajes
Realizar gráficos de barras
¿Cómo se relacionan con el contexto del problema?

De acuerdo con la información del problema contesta las siguientes preguntas:

1. ¿Se puede conocer el incremento o decremento para los estudiantes de reingreso del ciclo 2015-2016? ¿Por qué?

2. ¿Qué operación te ayudaría para conocer el porcentaje de incremento o decremento?

3. ¿Este resultado está expresado en forma de porcentaje? ¿Qué otras operaciones se necesitan realizar?

4. Para el incremento o decremento del ciclo escolar 2016-2017, ¿qué operación debes realizar?

5. Para los siguientes ciclos escolares, ¿Cuáles son los porcentajes de incrementos o decrementos?

6. Al graficar ¿cuáles datos debes colocar en el eje de las abscisas y cuales en el eje de las ordenadas?

7. Traza la gráfica con la información que obtuviste anteriormente.

Lecturas:

Rodríguez, M. (coord), Chávez, N., Martínez, U., Ochoa, G., Ramírez, J. Ramírez, E., Ramírez, N., Sánchez R., Sandoval, M., Soriano, R. (autores)
(2020). Matemáticas IV: Guía cuaderno de trabajo académico. ENP, UNAM

FES Cuautitlán-UNAM (s/f). Gráficas de barras. México. Recuperado de: https://bit.ly/2UyCqO3

Video:

Daniel Carreón (2017). Como hacer una gráfica de barras súper fácil. [Archivo de video]. Recuperado de: https://bit.ly/2MUHurO

1.2. Parte 2. Lenguaje y expresiones algebraicas.

Objetivo

El estudiante:

Utilizará los contenidos de representación de información numérica en traducción de ideas al lenguaje algebraico para resolver problemas contextualizados.

Productos esperados

Solución a un problema

Recursos

Guía de estudios de Matemáticas IV
Videos de YouTube

Actividad de aprendizaje

Materiales

Forma de trabajo: Individual

Indicaciones

1. Lee cuidadosamente y contesta las preguntas planteadas a partir de tus conocimientos y los recursos de apoyo que se te proporcionan.

Si $n$ es la población escolar total y $m$ es el porcentaje de mujeres, ¿cuál expresión puedes utilizar para determinar el número de estudiantes hombres en un ciclo escolar determinado?

Para dar solución al problema revisa los siguientes materiales:

Presta atención en lo siguiente:

Lenguaje y expresiones algebraicas
¿Cómo se relacionan con el contexto del problema?

De acuerdo con la información del problema contesta las siguientes preguntas:

1. ¿Cómo expresas el porcentaje en valor decimal?

2. Si $m$ es el porcentaje de mujeres, ¿cómo expresas este valor en número decimal?

3. A partir de lo anterior, ¿cómo calcularías el porcentaje de estudiantes hombres que se tiene?

4. Si $n$ es la población escolar total, ¿qué expresión utilizas para conocer el número de hombres que se tiene?

Lecturas:

Rodríguez, M. (coord), Chávez, N., Martínez, U., Ochoa,
G., Ramírez, J. Ramírez, E., Ramírez, N., Sánchez R.,
Sandoval, M., Soriano, R. (autores) (2020).
Matemáticas IV: Guía cuaderno de trabajo académico.
ENP, UNAM

Portal Académico CCH. (2018). Lenguaje algebraico.
Colegio de Ciencias y Humanidades, UNAM.
Recuperado de: https://bit.ly/3hmLFdY

Video:

Matemáticas profe Alex. (2018). Lenguaje algebraico. Parte 1 [Archivo de video]. Recuperado de: https://bit.ly/2C3fuA7

1.3. Parte 3. Funciones.

Objetivo

El estudiante:

Usará los contenidos de representación de información numérica en la modelación de situaciones mediante funciones para resolver problemas contextualizados.

Productos esperados

Solución a un problema

Recursos

Guía de estudios de Matemáticas IV
Videos de YouTube

Actividad de aprendizaje

Materiales

Forma de trabajo: Individual

Indicaciones

1. Lee cuidadosamente y contesta las preguntas planteadas a partir de tus conocimientos y los recursos de apoyo que se te proporcionan.

En el ciclo escolar 1999-2000 ingresaron 32,530 alumnos, mientras que en el ciclo escolar 2019-2020 ingresaron 35,041 alumnos al bachillerato UNAM.

Suponiendo que se tuviera un comportamiento lineal y creciente, modelado por la función $f(p)=125.55p+32530$ , donde $p$ es el tiempo en años transcurridos desde el ciclo escolar 1999-2000, ¿cuántos alumnos se atenderían durante el ciclo escolar 2029-2030?

Para dar solución al problema revisa los siguientes materiales:

Poner la lista de materiales que se deben revisar (columna el lado derecho de documento en word)

Presta atención en lo siguiente:

Conceptos de función
Evaluar una función
¿Cómo se relacionan con el contexto del problema?

De acuerdo con la información del problema contesta las siguientes preguntas:

1. Si $p=0$ , ¿qué valor se obtiene? y ¿qué representa?

2. Para el ciclo 2019-2020, ¿cuál es el valor de $p$ ?

3. Para el ciclo 2029-2030, ¿cuál será el valor de $p$ ?

4. Al evaluar en la función el valor de

$p$ para el ciclo 2029-2030, ¿cuál es el resultado?

Lecturas:

Rodríguez, M. (coord), Chávez, N., Martínez, U., Ochoa,
G., Ramírez, J. Ramírez, E., Ramírez, N., Sánchez R., Sandoval, M., Soriano, R. (autores) (2020). Matemáticas IV: Guía cuaderno de trabajo académico. ENP, UNAM

B@unam. (2017). Funciones y su representación gráfica. CUAED-UNAM. Recuperado de: https://bit.ly/3cUz51V

Video:

Laracos Math (2011). Como evaluar funciones lineales [Archivo de video]. Recuperado de: https://bit.ly/2Am09dx

1.4. Parte 4. Sistemas de ecuaciones lineales de 2x2.

Objetivo

El estudiante:

Usará los contenidos de representación de información numérica en la resolución de sistemas de ecuaciones lineales para resolver problemas contextualizados.

Productos esperados

Solución a un problema

Recursos

Guía de estudios de Matemáticas IV
Videos de YouTube

Actividad de aprendizaje

Materiales

Forma de trabajo: Individual

Indicaciones

1. Lee cuidadosamente y contesta las preguntas planteadas a partir de tus conocimientos y los recursos de apoyo que se te proporcionan.

En el ciclo escolar de 2018 a 2019, egresaron 29335 estudiantes en total. Si al triple de alumnos que egresaron de la ENP se le resta el doble de alumnos que egresaron del CCH, se tiene 9 820 alumnos, ¿cuántos alumnos egresaron de la ENP en dicho ciclo?

Para dar solución al problema revisa los siguientes materiales:

Presta atención en lo siguiente:

Sistemas de ecuaciones lineales de 2x2
Métodos de solución de sistemas de ecuaciones lineales de 2x2
¿Cómo se relacionan con el contexto del problema?

De acuerdo con la información del problema contesta las siguientes preguntas:

1. ¿Qué procedimiento matemático puedes utilizar para modelar el problema?

2. Al utilizar $x$ para el número de alumnos de la ENP y $y$ como el número alumnos del CCH: ¿Cómo traduces a lenguaje matemático el siguiente enunciado: En el ciclo escolar de 2018 a 2019, egresaron 29 335 estudiantes en total?

3. ¿Cómo traduces a lenguaje matemático el siguiente enunciado: al triple de alumnos que egresaron de la ENP se le resta el doble de alumnos que egresaron del CCH, se tiene 9 820 alumnos?

4. De lo anterior puedes formar un sistema de ecuaciones de 2X2, al resolverlo por el método de tu elección obtienes:

5. ¿Cuántos alumnos egresaron de la ENP en dicho ciclo?

Lecturas:
Rodríguez, M. (coord), Chávez, N., Martínez, U., Ochoa, G.,
Ramírez, J. Ramírez, E., Ramírez, N., Sánchez R., Sandoval, M., Soriano, R. (autores) (2020). Matemáticas IV: Guía cuaderno de trabajo académico. ENP, UNAM

Martín, A. (s/f). Sistemas de ecuaciones lineales. Proyecto Descartes. Ministerio de Educación, Cultura y Deportes de España. Recuperado de: https://bit.ly/3e47lJW

math2me (2019). Plantear Problemas de sistemas de ecuaciones lineales 2x2. [Archivo de video]. Recuperado de: https://bit.ly/2Yyugqd

1.5. Parte 5. Inecuación lineal en dos variables.

Objetivo

El estudiante:

Utilizará los contenidos de representación de información numérica en inecuaciones de primer grado con dos variables para resolver problemas contextualizados.

Productos esperados

Solución a un problema

Recursos

Guía de estudios de Matemáticas IV
Videos de YouTube

Actividad de aprendizaje

Materiales

Forma de trabajo: Individual

Indicaciones

1. Lee cuidadosamente y contesta las preguntas planteadas a partir de tus conocimientos y los recursos de apoyo que se te proporcionan.

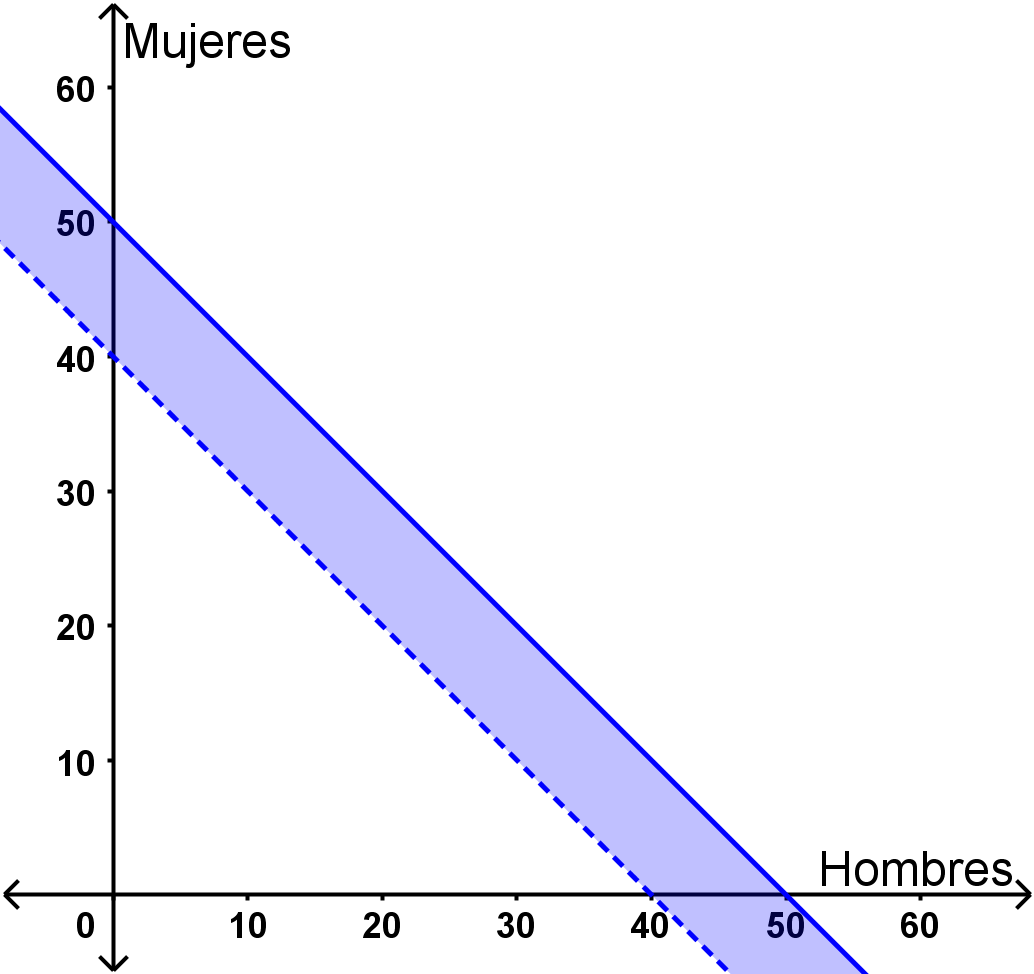
El siguiente grafico muestra la distribución de alumnos de nuevo ingreso por salón de clases en uno de los planteles de la ENP:

Si $x$ representa el número de hombres y $y$ el número de mujeres por salón de clases, indica una inecuación que modele el problema.

Para dar solución al problema revisa los siguientes materiales:

Presta atención en lo siguiente:

Inecuación lineal en dos variables
Graficar una inecuación lineal en dos variables
¿Cómo se relacionan con el contexto del problema?

De acuerdo con la información del problema contesta las siguientes preguntas:

1. En la gráfica, ¿qué significado tiene la región sombreada?

2. ¿Qué significa que una línea sea punteada y otra continua?

3. ¿Todos los puntos de la región sombreada pertenecen a la solución de acuerdo con el contexto del problema?

4. ¿Cuál es el número máximo y mínimo de estudiantes que se puede tener por salón?

5. ¿Existe la posibilidad, de acuerdo con el gráfico, de que haya 0 hombres o 0 mujeres en un salón?

6. ¿Qué expresión algebraica modela el número de hombres y mujeres que asisten a un mismo salón?

7. Al aplicar las restricciones antes vistas, ¿qué inecuación modela el problema?

Lecturas:

Rodríguez, M. (coord), Chávez, N., Martínez, U., Ochoa,
G., Ramírez, J. Ramírez, E., Ramírez, N., Sánchez R.,
Sandoval, M.,Soriano, R. (autores) (2020). Matemáticas IV:
Guía cuaderno de trabajo
académico. ENP, UNAM

cidead (s/f). Inecuaciones. Centro para la Innovación y Desarrollo de la Educación a Distancia. España.
Recuperado de: https://bit.ly/3e4aUji

Video:

KhanAcademyEspañol (2013). Graficando desigualdades lineales en dos variables 3 [Archivo de video].
Recuperado de: https://bit.ly/3fkpwey

1.6. Referencias

Lecturas:

B@unam. (2017). Funciones y su representación gráfica.CUAED-UNAM. Recuperado de http://uapas1.bunam.unam.mx/matematicas/funciones_y_su_representacion_grafica/

cidead (s/f). Inecuaciones. Centro para la Innovación y Desarrollo de la Educación a Distancia. Recuperado de: http://recursostic.educacion.es/secundaria/edad/4esomatematicasB/inecuaciones/impresos/quincena5.pdf

FES Cuautitlán-UNAM. (s/f). Gráficas de barras. México. Recuperado de http://asesorias.cuautitlan2.unam.mx/Laboratoriovirtualdeestadistica/DOCUMENTOS/TEMA%201/6.%20GRAFICA%20DE%20BARRAS.pdf

Martín, A. (s/f). Sistemas de ecuaciones lineales. Proyecto Descartes. Recuperado de: http://recursostic.educacion.es/descartes/web/materiales_didacticos/Sistemas_ecuaciones_lineales/Sistemas_de_ecuaciones_lineales.htm

Portal Académico CCH. (2018). Lenguaje algebraico. Colegio de Ciencias y Humanidades, UNAM. Recuperado de: https://portalacademico.cch.unam.mx/alumno/matematicas1/unidad3/lenguajealgebraico

Rodríguez, M. (coord), Chávez, N., Martínez, U., Ochoa, G., Ramírez, J. Ramírez, E., Ramírez, N., Sánchez R., Sandoval, M., Soriano, R. (autores) (2020). Matemáticas IV: Guía cuaderno de trabajo académico. ENP, UNAM.

Videos:

Daniel Carreón. (2017). Cómo hacer una gráfica de barras súper fácil. [Archivo de video]. Recuperado de: https://www.youtube.com/watch?v=J-lDNbXM2wE

KhanAcademyEspañol (2013). Graficando desigualdades lineales en dos variables 3. [Archivo de video]. Recuperado de: https://youtu.be/tpi-qwgXIZs

Laracos Math (2011). Cómo evaluar funciones lineales. [Archivo de video]. Recuperado de: https://www.youtube.com/watch?v=H62e5s5ODcs

Matemáticas profe Alex. (2018). Lenguaje algebraico. Parte 1. [Archivo de video]. Recuperado de: https://www.youtube.com/watch?v=DV3C_RawfBg&t=552s

math2me] (2019). Plantear Problemas de sistemas de ecuaciones lineales 2x2. [Archivo de video]. Recuperado de: https://www.youtube.com/watch?v=gd95JhLC4LU