libro digital

Sitio:	Tu Aula Virtual
Curso:	Curso: Blanca Estela García Rojas -Conceptos de Ingeniería
Libro:	libro digital

Impreso por:	Invitado
Fecha:	miércoles, 10 de diciembre de 2025, 04:05

Descripción

Tabla de Contenidos

1. Vectores

1. Vectores

1.1. Clasificación de cantidades vectoriales y escalares

Para expresar los fenómenos físicos o químicos que ocurren en la naturaleza o en los equipos de ingeniería es necesario hacerlo a través de los cambios que sufren las variables que rigen a estos fenómenos. Estas variables las podemos clasificar en:

Cantidades Escalares
Cantidades Vectoriales
Las cantidades escalares se caracterizan por ser descritas a plenitud a través de un número. Ejemplos de cantidades escalares son: la presión, la temperatura, la densidad, etc.

En cambio las cantidades vectoriales para describirlas por completo es necesario señalar su magnitud, su dirección y sentido.
Ejemplos, de cantidades vectoriales son:
La velocidad
La aceleración
La fuerza

Para distinguir si se esta hablando de un vector o de un escalar se requiere de una nomenclatura que permita hacer una diferencia entre las dos cantidades. Entonces, cuando se hace referencia a un escalar simplemente se utiliza una letra que se relacione con la variable de la se está hablando, por ejemplo para la presión se usa sencillamente la letra P; mientras que si se habla de un vector suele utilizarse una letra con una flecha por encima de ella, por ejemplo el vector fuerza podría expresarse como $\vec{F}$ , aunque también suele utilizarse una letra en negrita para referirnos a un vector, ejemplo F. Parte también de la nomenclatura vectorial es que la magnitud del vector se representa como el vector encerrado entre el símbolo de valor absoluto $\left| \begin{matrix}\vec{F} \end{matrix} \right|$ .

1.2. Representación de las cantidades vectoriales

Representación gráfica

Existen diferentes maneras de representar a un vector, una de ellas es a través de una flecha. La longitud de la flecha está relacionada con la magnitud del vector y la inclinación con respecto a los ejes de coordenadas indican la dirección; finalmente el sentido esta indicado por la punta de la flecha.

El vector puede colocarse sobre el plano cartesiano en la cual se traza la flecha con cierta longitud y dirección con respecto al este plano. Estos vectores que se encuentran contenidos en un espacio bidimensional pueden tener 1 o 2 componentes, donde los componentes serán proyecciones del vector sobre los ejes de coordenadas que forman al plano cartesiano.

Para trazar el vector es necesario elegir una escala en la que una unidad de la escala corresponda a una unidad del vector. Así por ejemplo, si queremos representar un vector cuya magnitud sea 5 y tenga una dirección de 37 ° con respecto al eje x, podemos elegir como escala longitudinal en la que cada centímetro represente una unidad del vector y con la ayuda de una regla y un transportador trazar una flecha de 5 cm de longitud y con 37° de inclinación con respecto a uno de los ejes de coordenadas.

Los vectores vectores no sólo están contenidos en un espacio bidimensional, como en un plano xy, sino que también pueden estar situados en el espacio tridimensional. Para representar el vector en un sistema tridimensional es necesario visualizar dos secciones planas dentro de los ejes coordenados. en uno de los planos se encontrará encerrado el vector y tendrá cierta inclinación con respecto a uno de los ejes de coordenadas, ver figura, y el segundo plano contendrá la proyección del vector sobre ese plano, línea punteada en la figura, el ángulo que se forma con respecto a otro de los ejes permite también trazar el vector en un sistema tridimensional. Un vector que se encuentra contenido en un espacio tridimensional puede tener 1, 2 o 3 componentes.

Representación del vector a través de sus componentes

Los vectores también suelen representarse a través de sus componentes, las componentes de un vector tienen un valor numérico asignado que depende de la dirección del vector. En este caso la representación del vector es la siguiente:

$\vec{a}=( a_x,a_y)$ para un vector bedimensional y $\vec{a}=( a_x,a_y, a_z)$ para un vector tridimensional.
Donde $a_x, a_y$ y $a_z$ tienen asignados valores numéricos.

1.3. Representación gráfica de las componentes de un vector

Las componentes de un vector se pueden visualizar como la proyección del vector sobre los ejes de coordenadas. Podríamos aterrizar esta idea si pensamos que el vector puede ser representado en la vida real a través de un segmento de madera y lo colocamos con cierto grado de inclinación sobre una superficie, después colocamos una lampara sobre el segmento de madera y observamos la sombra que produce el vector sobre una línea de la superficie (eje de coordenadas) sobre la que se proyecta el vector.

Para determinar de manera gráfica las componentes del vector (es decir sus proyecciones sobre los ejes) primero debemos elegir una escala en la que una unidad de la escala corresponda a una unidad de la magnitud del vector, después trazar las unidades del vector, según la escala elegida, en seguida trazar líneas rectas paralelas a los ejes de coordenadas que irán desde la punta del vector hasta tocar los ejes de tal manera que encerremos en un paralelogramo al vector el valor en la intersección entre la línea recta con los ejes de coordenadas serán las componentes del vector.

Ejemplo:

Para obtener de manera gráfica las componentes de una fuerza cuya magnitud es de 5 N y su dirección de 37° con respecto al eje horizontal, elegimos primero como escala que 1cm = 1N entonces trazamos, con la ayuda de una regla, una flecha de 5cm y después las líneas rectas perpendiculares a los ejes.

De esta manera el vector también se puede representar a través de los valores de estas proyecciones sobre los ejes, por ejemplo:

$\vec{F}$ =(F_x, F_y)=(4,3)

donde F_x es la componente de la fuerza sobre el eje x y F_y es la componente de la fuerza sobre el eje y.

También lo podemos escribir en forma de columna.

$\vec{F}$ = $\binom {Fx}{Fy}$ = $\binom {4} {3}$

La proyección del vector sobre los ejes coordenados depende de el grado de inclinación del vector con respecto al eje; entre más cerca esté el vector del eje de coordenadas mayor es la proyección este sobre dicho eje y tendrá menor proyección sobre el otro eje.

1.4. Vectores unitarios y normalización de un vector

Vector unitario

Los vectores unitarios son aquellos cuya magnitud tiene como valor al unidad. En general para representarlo se utiliza una letra la cual tiene encima de ella un símbolo circunflejo, por ejemplo, $\hat{a}$

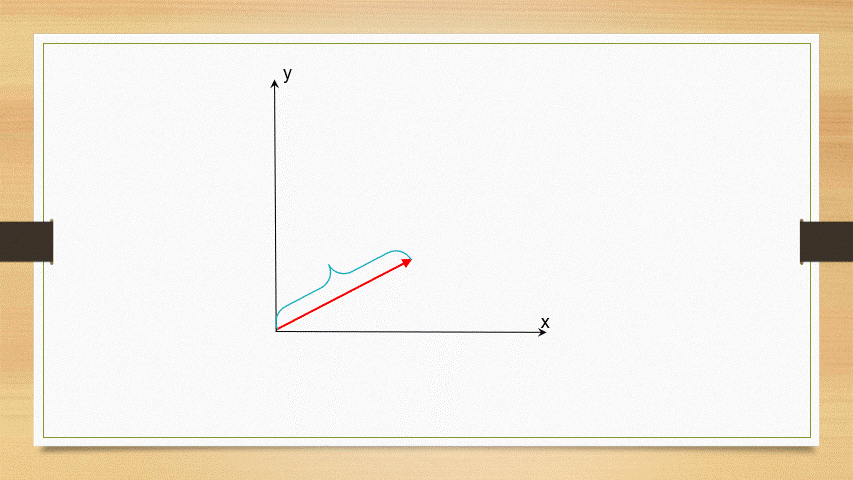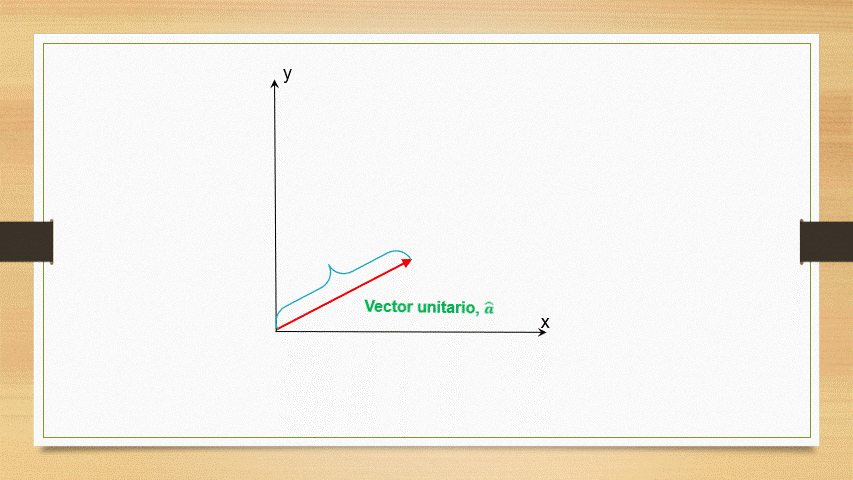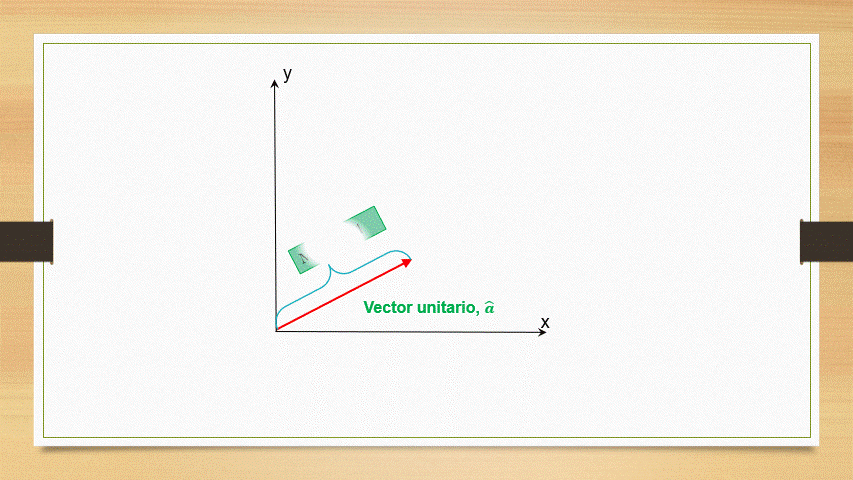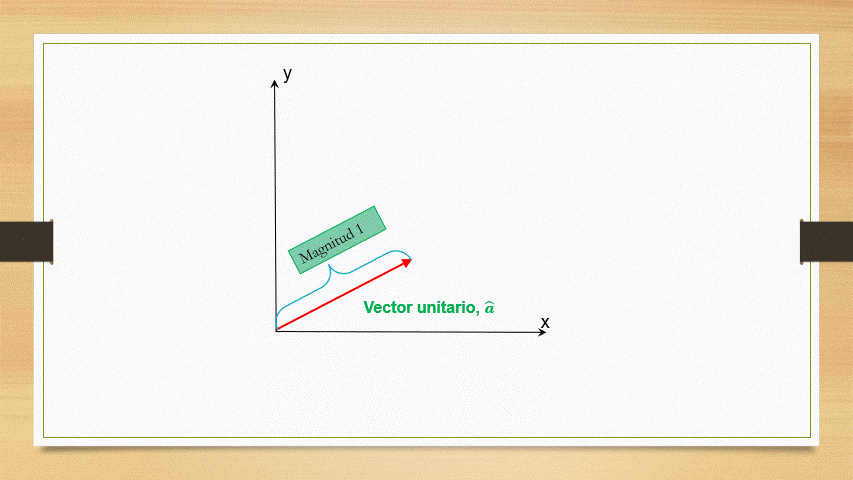
En física se conocen 3 vectores unitarios que tiene respectivamente la dirección del eje x,

$\hat{\imath}$ =(1,0,0), el eje y, $\hat{\jmath}$ =(0,1,0) y el eje z, $\hat{k}$ =(0,0,1). Además estos vectores son ortogonales entre si por esas dos características son llamados vectores ortonormales.

Normalización de un vector

Cuando hablamos de normalizar un vector nos referimos a que a partir de este vamos a obtener un vector unitario cuya dirección y sentido serán los mismos que la del vector original. Para llevar a cabo la normalización es necesario conocer la magnitud del vector y sus componentes. Por ejemplo, supongamos que tenemos un vector de magnitud $\left| \vec{a} \right|$ , y cuyas componentes se conocen y son $\vec{a}=(a_x, a_y, a_z)$ . Entonces, el vector unitario asociado a $\vec{a}$ será:

$\hat{a}$ = $(\frac{a_x}{\left| \begin{matrix} \vec{a} \end{matrix} \right| }\hat{i}, \frac{a_y}{\left| \begin{matrix} \vec{a} \end{matrix} \right| }\hat{j}, \frac{a_z}{\left| \begin{matrix} \vec{a} \end{matrix} \right| }\hat{k})$ .

Ejemplo:

Normalice el vector $\vec{a}$ cuyas componentes son (4 $\hat{i}$ ,-3 $\hat{j}$ ,5 $\hat{k}$ ) .

Determinar la magnitud del vector a través de sus componentes
Dividir cada componente entre la magnitud que se determino en el paso previo.
$\left| \begin{matrix} \vec{a} \end{matrix} \right| = \sqrt[2]{(4)^2+(-3)^2+(5)^2} =7.071$

Entonces el vector $\vec{a}$ normalizado es:

$\hat{a}$ = $(\frac{-4}{7.071}\hat{i}, \frac{-3}{7.071}\hat{j}, \frac{5}{7.071}\hat{k})$

$\hat{a}$ =(0.5657 $\hat{i}$ ,-0.4243 $\hat{j}$ ,0.7071 $\hat{k}$ )

Si determinamos la magnitud de este vector veremos que es de aproximadamente 1.

1.5. Determinación de la magnitud de un vector y sus componentes en dos dimensiones

Determinación de la magnitud de un vector

Si se conocen los valores de las componentes de un vector es muy sencillo determinar su magnitud. Como ejemplo tomaremos un vector, $\vec{a}$ cuyas componentes son $a_x$ =-3 y $a_y$ =5. Para mostrar como determinar la magnitud del vector, primero se representará el vector en el plano cartesiano. Si trazamos líneas paralelas a los ejes de coordenadas (líneas punteadas color verde), el vector queda encerrado en un paralelo gramo, en este paralelogramo se puede observar un triángulo rectángulo formado por las componentes del vector (-3,5) que son los catetos del triángulo y por la magnitud del vector que es la hipotenusa.

Entonces, se puede utilizar el teorema de Pitágoras para determinar la magnitud.

$\left| \begin{matrix} \vec{a} \end{matrix} \right|$ = $\sqrt[2]{(a_x)^2+(a_y)^2}$ = $\sqrt[2]{(-3)^2+(5)^2} =5.83$

Determinación de las componentes de un vector

Si lo que se conoce es la magnitud del vector y su dirección (ángulo de inclinación con respecto a alguno de los ejes) entonces es posible determinar de manera numérica, a través de estos datos, las componentes del vector. Como se menciona en las sección anterior la magnitud del vector y las componentes de este forman un triángulo rectángulo en la que las componentes son los catetos y la magnitud la hipotenusa del triángulo. Por lo que, utilizando las funciones trigonométricas seno y coseno, que relacionan los catetos y la hipotenusa del triángulo, podemos despejar los catetos, es decir, las componentes del vector.

En el gráfica superior vemos que $a_x$ es el cateto adyacente al ángulo β, por lo que usando la función cos(β), que es igual al cateto adyasente entre la hipotenusa, y despejando $a_x$ se obtiene la componente del vector sobre el eje "x".

$cos( \beta)$ = $\frac{a_x}{\left| \begin{matrix} \vec{a} \end{matrix} \right| }$

$a_x$ =- $\left| \begin{matrix} \vec{a} \end{matrix} \right|$ $cos(\beta)$

De igual manera obtiene la componente $a_y$ del vector, pero ahora usando la función seno $\beta$ que relaciona al catero opuesto entre la hipotenusa.

$sen( \beta)$ = $\frac{a_y}{\left| \begin{matrix} \vec{a} \end{matrix} \right| }$

$a_y$ = $\left| \begin{matrix} \vec{a} \end{matrix} \right|$ $sen(\beta)$ .

El signo menos que aparece en lal componente "x" del vector $\vec{a}$ se intoduce a la ecuación ya que, como muestra la figura, el vector esta situado en el segundo cuadrante del plano cartesiano, entonces la proyección del vector esta sobre los valores negativos del eje "x" y sobre los valores positivos del eje "y". Otra manera de obtener de forma directa el signo de las componentes es utilizar como argumento de las funciones coseno y seno el ángulo suplementario del ángulo $\beta$ , es decir, 180- $\beta$ .

Ejemplo:

Determine las componentes del vector fuerza que se muestra en la siguiente figura.

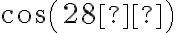$F_x$ = $\left| \begin{matrix} 6 \end{matrix} \right|$ $cos(28°)$ =5.3 N

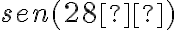$F_y$ =- $\left| \begin{matrix} 6 \end{matrix} \right|$ $sen(28°)$ =-2.83 N

1.6. Determinación de las componentes de un vector en 3 dimensiones

Un vector en tres dimensiones está inmerso en un plano que se encuentra desplazado a lo largo uno de los ejes coordenados, ver figura. Este vector tendrá entonces 3 componentes sobre los ejes x, y, z.

Para determinar las componentes del vector haremos uso de dos triángulos rectángulos, el primero se encuentra inmerso en el plano que se ha desplazado α grados a lo largo del eje z, ver figura inferior. En este primer triángulo rectngulo la magnitud del vector es la hipotenusa, que tiene un ángulo de inclinación β con respecto al eje y. El cateto adyacente a este ángulo es la componente $y$ del vector, mientras que el cateto opuesto a este ángulo, identificado aquí como $m$ , es la proyección del vector pero sobre el plano $xz$ . Esta proyección es ahora la hipotenusa del segundo triágulo rectángulo que se encuentra sobre el plano $xz$ , los catetos de este segundo triángulo son las componentes $x$ y $z$ del vector.

Entonces, para el primer triángulo rectángulo:

Componente $y$ del vector

$b_y= \left| \begin{matrix} \vec{b} \end{matrix} \right| cos( \beta)$

Proyección del vector sobre el plano $xz$

$m= \left| \begin{matrix} \vec{b} \end{matrix} \right| sen( \beta)$

Del segundo triángulo:

Componente $x$ del vector

$b_x=mcos( \alpha) = \left| \begin{matrix} \vec{b} \end{matrix} \right| sen( \beta )cos( \alpha)$

Componente $z$ del vector

$b_z= msen( \alpha )=\left| \begin{matrix} \vec{b} \end{matrix} \right| sen(\beta )sen(\alpha )$

Ejemplo:

Determine las componentes del vector fuerza que se muestra en la figura.

$F_y= \left| \begin{matrix} 40 \end{matrix} \right| cos( 30°) = 34.64 N$

$F_x=\left| \begin{matrix} 40 \end{matrix} \right| sen( 30° )cos( 50° ) = 12.86 N$

$F_z=\left| \begin{matrix} 40 \end{matrix} \right| sen( 30° )sen( 50° ) = 15.32 N$

1.7. Suma de vectores

Suma de vectores

La suma de vectores da como resultado un nuevo vector, esta operación se realiza componente a componente. Entonces para realizar una suma vectorial es necesario conocer o determinar las componentes de los vectores.

Su pongamos que se tienen dos vectores $\vec{\text{a}}$ y $\vec{\text{b}}$ , cuyas componentes son $(\text{a}_x,\text{a}_y,\text{a}_z)$ y $(\text{b}_x,\text{b}_y,\text{b}_z)$ respectivamente.Entonces la suma vectorial se realiza de la siguiente manera:

$\vec{\text{a}}$ + $\vec{\text{b}}$ = ( $\text{a}_x +\text{b}_x, \text{ a}_y +\text{b}_y, \text{a}_z +\text{b}_z$ )

Ejemplo:

Propiedades de la suma vectorial

Las propiedades de la suma vectorial son las siguientes:

1.- Asociativa

Nos indica que cuando se suman dos o más vectores el resultado es el mismo sin importar la forma quen que son agrupados.

\begin{align}\overset{\rightarrow}{\text{a}} + \left( \overset{\rightarrow}{\text{b}} +
\overset{\rightarrow}{\text{c}} \right) = \left(
\overset{\rightarrow}{\text{a}} + \overset{\rightarrow}{\text{b}} \right) +
\overset{\rightarrow}{\text{c}}\end{align}

2.- Conmutativa

En esta propiedad se establece que el orden de los sumandos no altera el resultado.

\begin{align}\overset{\rightarrow}{\text{a}} + \overset{\rightarrow}{\text{b}} =
\overset{\rightarrow}{\text{b}} + \overset{\rightarrow}{\text{a}}\end{align}

3.- Elemento opuesto

Para cualquier vector $\vec{\text{a}}$ existe un vector - $\vec{\text{a}}$ que sumados dan como resultado el vector nulo, este vector se denomina vector opuesto y es único para el vector $\vec{\text{a}}$ .

\begin{align}\overset{\rightarrow}{\text{a}} + \left( – \overset{\rightarrow}{\text{a}}
\right) = \overset{\rightarrow}{\text{0}}\end{align}

4.- Elemento neutro

Existe un vector nulo que sumado con un vector da como resultado el mismo vector.

\begin{align}\overset{\rightarrow}{\text{a}} + \overset{\rightarrow}{\text{0}} =
\overset{\rightarrow}{\text{a}}\end{align}

1.8. Producto punto o producto escalar entre vectores

Producto punto

El producto punto es otra de las operaciones que se realiza entre vectores y da como resultado una cantidad escalar, se representa mediante un punto entre los vectores involucrados, $\vec{a} \bullet \vec{b}$ . Su interpretación gráfica es la proyección que tiene un vector sobre otro.

Existen dos formas de obtener ese valor escalar de la proyección entre vectores. Una de ellas se realiza facilmente si se conocen las magnitudes de los vectores involucrados y el ángulo que existe entre ellos, en la figura superior este ángulo esta representado como $\beta$ .

| $\vec{a}$ $\bullet$ $\vec{b}$ | =| $\vec{a}$ || $\vec{b}$ | cos( $\beta)$

También se puede obtener el valor del producto punto entre los vectores si se conocen las componentes de cada vector, la manera de proceder es multiplicar componente a componente y sumar el resultado de esos productos.

$\vec{a}$ $\bullet$ $\vec{b}$ = $a_x$ $b_x$ + $a_y$ $b_y$ + $a_z$ $b_z$ .

Ejemplo:

Si las componentes del vector $\vec{a}$ son (5 $\hat{i}$ , -4 $\hat{j}$ , 1 $\hat{k}$ ) y las del vector $\vec{b}$ son (-1 $\hat{i}$ , 3 $\hat{j}$ , 4 $\hat{k}$ ) de termine, $\vec{a}$ $\bullet$ $\vec{b}$ .

| $\vec{a}$ $\bullet$ $\vec{b}$ | = |(5)(-1)+(-4)(3)+(1)(4)|=|-13|=13

Propiedades de producto punto

Comutativa

$\vec{a}$ $\bullet$ $\vec{b}$ = $\vec{b}$ $\bullet$ $\vec{a}$

Asociativa

k(( $\vec{a}$ $\bullet$ $\vec{b}$ )=( $k\vec{a}$ ) $\bullet$ $\vec{b}$

donde k es una cantidad escalar.

Distributiva

$\vec{c}$ $\bullet$ ( $\vec{a}$ + $\vec{b}$ )= $\vec{c}$ $\bullet$ $\vec{a}$ + $\vec{c}$ $\bullet$ $\vec{b}$

1.9. Producto cruz entre vectores

El producto cruz es otra de la operaciones vectoriales básicas que se lleva a cabo entre vectores. El producto cruz da como resultado un nuevo vector que es perpendicular al plano en el que se encuentran los vectores involucrados en la operación. Por ejemplo $\vec{a}$ x $\vec{b}$ da como resultado el vector $\vec{c}$ , ver figura.

La magnitud del vector $\vec{c}$ se obtiene haciendo la siguiente operación:

$\vec{c}$ =| $\vec{a}$ | | $\vec{b}$ | sen( $\beta$ )

La dirección y sentido del vector $\vec{c}$ deberá obtenerse con la regla de la mano derecha

Regla de la mano derecha

Para llevar a cabo la regla de la mano derecha tenemos que utilizar el dedo indice, el dedo medio y el dedo pulgar. Gire su mano derecha de tal manera que el dedo índice esté alineado y apuntando en el sentido del primer vector, en este caso vector a, el dedo medio debe apuntar en la dirección del vector b, finalmente el dedo pulgar apuntará en la dirección del vector resultante.

El producto vectorial también se representa de forma compacta por medio de un determinante que para el caso de dimensión 3×3 es :

c=axb= $\left| \begin{matrix} \hat{i} & \hat{j} & \hat{k} \\ a_x & a_y & \ a_z \\ b_x & b_y & b_z\end{matrix} \right|$ = $[ (a_y b_z)- (a_z b_y) ] \hat{i}- [ (a_x b_z)- (a_z b_x) ] \hat{j}+ [ (a_x b_y)- (a_y b_x) ] \hat{k}$

Ejemplo

Si las componentes del vector $\vec{a}$ son (3 $\hat{i}$ , -2 $\hat{j}$ , 1 $\hat{k}$ ) y las del vector $\vec{b}$ son (5 $\hat{i}$ , -4 $\hat{j}$ , 3 $\hat{k}$ ) de termine, $\vec{a}$ x $\vec{b}$ .

$\vec{c}$ = $\vec{a}$ x $\vec{b}$ = $\left| \begin{matrix} \hat{i} & \hat{j} & \hat{k} \\ 3 & -2 & 1\\ 5 & -4 & 3\end{matrix} \right|$ = $[ (-2)(3)- (1)(-4)] \hat{i}- [ (3)(3)- (1) (5) ] \hat{j}+ [ (3) (-4)- (-2)(5) ] \hat{k}$

Entonces las componentes del nuevo vector que resulta de $\vec{a}$ x $\vec{b}$ es:

$\vec{c} =-2\hat{i}+4\hat{j}-2\hat{k}$

1.10. Producto diádico

Es posible definir un tercer producto que tiene carácter tensorial. Este producto diádico (o tensorial) puede representarse en coordenadas cartesianas por una matriz 3×3 cuyos elementos son los productos de las respectivas componentes.

$\begin{equation} \begin{pmatrix} A_{x}B_{x} & A_{x}B_{y} & A_{x}B_{z}\\ A_{y}B_{x} & A_{y}B_{y} & A_{y}B_{z}\\ A_{z}B_{x} & A_{z}B_{y} & A_{z}B_{z}\\ \end{pmatrix} \end{equation}$

El producto diádico se indica sin punto, ${ \vec{A}}{ \vec{B}}$ . También se representa con el símbolo de producto tensorial como $\vec{A} \otimes \vec{B}$ .

Esta matrix de 3x3 se le conoce como tensor de segundo orden y puede obtenerse a partir de un vector fila y un vector columna.

\begin{equation}( \vec{A} \vec{B} ) = \begin{pmatrix} A_{x} & A_{y} & A_{z} \end{pmatrix} \begin{pmatrix} B_{x} \\ B_{y} \\ B_{z} \end{pmatrix}\end{equation}

Propiedades del producto diádico

Linealidad

El producto diádico, así definido, es lineal respecto a los dos vectores que lo forman, esto es:

$\vec{A} ( \lambda \vec{B} +μ \vec{C} ) = ( \lambda\vec{A} \vec{B} +μ\vec{A} \vec{C} )$

Esta propiedad no es exclusiva de este producto. También el producto escalar y el vectorial la satisfacen.

Simetría o antisimetría

A diferencia del producto escalar, que es conmutativo, y del vectorial, que es anticonmutativo, el producto diádico no será.

$\vec{A} \vec{B} \neq \vec{B} \vec{A}$

libro digital

Descripción

Tabla de Contenidos

1. Vectores

1.1. Clasificación de cantidades vectoriales y escalares

Para expresar los fenómenos físicos o químicos que ocurren en la naturaleza o en los equipos de ingeniería es necesario hacerlo a través de los cambios que sufren las variables que rigen a estos fenómenos. Estas variables las podemos clasificar en:

1.2. Representación de las cantidades vectoriales

Representación gráfica

Representación del vector a través de sus componentes

Los vectores también suelen representarse a través de sus componentes, las componentes de un vector tienen un valor numérico asignado que depende de la dirección del vector. En este caso la representación del vector es la siguiente:

\vec{a}=( a_x,a_y) para un vector bedimensional y \vec{a}=( a_x,a_y, a_z) para un vector tridimensional.Donde a_x, a_y y a_z tienen asignados valores numéricos.

1.3. Representación gráfica de las componentes de un vector

Ejemplo:

De esta manera el vector también se puede representar a través de los valores de estas proyecciones sobre los ejes, por ejemplo:

\vec{F} =(Fx, Fy)=(4,3)

donde Fx es la componente de la fuerza sobre el eje x y Fy es la componente de la fuerza sobre el eje y.

También lo podemos escribir en forma de columna.

\vec{F} = \binom {Fx}{Fy} = \binom {4} {3}

La proyección del vector sobre los ejes coordenados depende de el grado de inclinación del vector con respecto al eje; entre más cerca esté el vector del eje de coordenadas mayor es la proyección este sobre dicho eje y tendrá menor proyección sobre el otro eje.

1.4. Vectores unitarios y normalización de un vector

Vector unitario

Los vectores unitarios son aquellos cuya magnitud tiene como valor al unidad. En general para representarlo se utiliza una letra la cual tiene encima de ella un símbolo circunflejo, por ejemplo, \hat{a}

En física se conocen 3 vectores unitarios que tiene respectivamente la dirección del eje x,

\hat{\imath}=(1,0,0), el eje y, \hat{\jmath}=(0,1,0) y el eje z, \hat{k}=(0,0,1). Además estos vectores son ortogonales entre si por esas dos características son llamados vectores ortonormales.

Normalización de un vector

\hat{a}= (\frac{a_x}{\left| \begin{matrix} \vec{a} \end{matrix} \right| }\hat{i}, \frac{a_y}{\left| \begin{matrix} \vec{a} \end{matrix} \right| }\hat{j}, \frac{a_z}{\left| \begin{matrix} \vec{a} \end{matrix} \right| }\hat{k}) .

Ejemplo:

Normalice el vector \vec{a} cuyas componentes son (4\hat{i},-3\hat{j},5\hat{k}) .

Determinar la magnitud del vector a través de sus componentesDividir cada componente entre la magnitud que se determino en el paso previo. \left| \begin{matrix} \vec{a} \end{matrix} \right| = \sqrt[2]{(4)^2+(-3)^2+(5)^2} =7.071 Entonces el vector \vec{a} normalizado es:

\hat{a}= (\frac{-4}{7.071}\hat{i}, \frac{-3}{7.071}\hat{j}, \frac{5}{7.071}\hat{k})

\hat{a}=(0.5657\hat{i},-0.4243\hat{j},0.7071\hat{k})

Si determinamos la magnitud de este vector veremos que es de aproximadamente 1.

1.5. Determinación de la magnitud de un vector y sus componentes en dos dimensiones

Determinación de la magnitud de un vector

Entonces, se puede utilizar el teorema de Pitágoras para determinar la magnitud.

\left| \begin{matrix} \vec{a} \end{matrix} \right|= \sqrt[2]{(a_x)^2+(a_y)^2}=\sqrt[2]{(-3)^2+(5)^2} =5.83

Determinación de las componentes de un vector

En el gráfica superior vemos que a_x es el cateto adyacente al ángulo β, por lo que usando la función cos(β), que es igual al cateto adyasente entre la hipotenusa, y despejando a_x se obtiene la componente del vector sobre el eje "x".

cos( \beta)= \frac{a_x}{\left| \begin{matrix} \vec{a} \end{matrix} \right| }

a_x=- \left| \begin{matrix} \vec{a} \end{matrix} \right|cos(\beta)

De igual manera obtiene la componente a_y del vector, pero ahora usando la función seno\beta que relaciona al catero opuesto entre la hipotenusa.

sen( \beta)= \frac{a_y}{\left| \begin{matrix} \vec{a} \end{matrix} \right| }

a_y= \left| \begin{matrix} \vec{a} \end{matrix} \right|sen(\beta).

Ejemplo:

Determine las componentes del vector fuerza que se muestra en la siguiente figura.

F_x= \left| \begin{matrix} 6 \end{matrix} \right|cos(28°)=5.3 N

F_y=- \left| \begin{matrix} 6 \end{matrix} \right|sen(28°)=-2.83 N

1.6. Determinación de las componentes de un vector en 3 dimensiones

Un vector en tres dimensiones está inmerso en un plano que se encuentra desplazado a lo largo uno de los ejes coordenados, ver figura. Este vector tendrá entonces 3 componentes sobre los ejes x, y, z.

Entonces, para el primer triángulo rectángulo:

Componente y del vector

b_y= \left| \begin{matrix} \vec{b} \end{matrix} \right| cos( \beta)

Proyección del vector sobre el plano xz

m= \left| \begin{matrix} \vec{b} \end{matrix} \right| sen( \beta)

Del segundo triángulo:

Componente x del vector

b_x=mcos( \alpha) = \left| \begin{matrix} \vec{b} \end{matrix} \right| sen( \beta )cos( \alpha)

Componente z del vector

b_z= msen( \alpha )=\left| \begin{matrix} \vec{b} \end{matrix} \right| sen(\beta )sen(\alpha )

Ejemplo:

Determine las componentes del vector fuerza que se muestra en la figura.

F_y= \left| \begin{matrix} 40 \end{matrix} \right| cos( 30°) = 34.64 N

F_x=\left| \begin{matrix} 40 \end{matrix} \right| sen( 30° )cos( 50° ) = 12.86 N

F_z=\left| \begin{matrix} 40 \end{matrix} \right| sen( 30° )sen( 50° ) = 15.32 N

1.7. Suma de vectores

Suma de vectores

La suma de vectores da como resultado un nuevo vector, esta operación se realiza componente a componente. Entonces para realizar una suma vectorial es necesario conocer o determinar las componentes de los vectores.

Su pongamos que se tienen dos vectores \vec{\text{a}} y \vec{\text{b}}, cuyas componentes son (\text{a}_x,\text{a}_y,\text{a}_z) y (\text{b}_x,\text{b}_y,\text{b}_z) respectivamente.Entonces la suma vectorial se realiza de la siguiente manera:

\vec{\text{a}} + \vec{\text{b}} = (\text{a}_x +\text{b}_x, \text{ a}_y +\text{b}_y, \text{a}_z +\text{b}_z )

Ejemplo:

Propiedades de la suma vectorial

Las propiedades de la suma vectorial son las siguientes:

1.- Asociativa

Nos indica que cuando se suman dos o más vectores el resultado es el mismo sin importar la forma quen que son agrupados.

\begin{align}\overset{\rightarrow}{\text{a}} + \left( \overset{\rightarrow}{\text{b}} + \overset{\rightarrow}{\text{c}} \right) = \left( \overset{\rightarrow}{\text{a}} + \overset{\rightarrow}{\text{b}} \right) + \overset{\rightarrow}{\text{c}}\end{align}

2.- Conmutativa

En esta propiedad se establece que el orden de los sumandos no altera el resultado.

\begin{align}\overset{\rightarrow}{\text{a}} + \overset{\rightarrow}{\text{b}} = \overset{\rightarrow}{\text{b}} + \overset{\rightarrow}{\text{a}}\end{align}

3.- Elemento opuesto

Para cualquier vector \vec{\text{a}} existe un vector -\vec{\text{a}} que sumados dan como resultado el vector nulo, este vector se denomina vector opuesto y es único para el vector \vec{\text{a}}.

$\vec{a}=( a_x,a_y)$ para un vector bedimensional y $\vec{a}=( a_x,a_y, a_z)$ para un vector tridimensional.
Donde $a_x, a_y$ y $a_z$ tienen asignados valores numéricos.

$\vec{F}$ =(F_x, F_y)=(4,3)

donde F_x es la componente de la fuerza sobre el eje x y F_y es la componente de la fuerza sobre el eje y.

$\vec{F}$ = $\binom {Fx}{Fy}$ = $\binom {4} {3}$

Los vectores unitarios son aquellos cuya magnitud tiene como valor al unidad. En general para representarlo se utiliza una letra la cual tiene encima de ella un símbolo circunflejo, por ejemplo, $\hat{a}$

$\hat{\imath}$ =(1,0,0), el eje y, $\hat{\jmath}$ =(0,1,0) y el eje z, $\hat{k}$ =(0,0,1). Además estos vectores son ortogonales entre si por esas dos características son llamados vectores ortonormales.

$\hat{a}$ = $(\frac{a_x}{\left| \begin{matrix} \vec{a} \end{matrix} \right| }\hat{i}, \frac{a_y}{\left| \begin{matrix} \vec{a} \end{matrix} \right| }\hat{j}, \frac{a_z}{\left| \begin{matrix} \vec{a} \end{matrix} \right| }\hat{k})$ .

Normalice el vector $\vec{a}$ cuyas componentes son (4 $\hat{i}$ ,-3 $\hat{j}$ ,5 $\hat{k}$ ) .

Determinar la magnitud del vector a través de sus componentes
Dividir cada componente entre la magnitud que se determino en el paso previo.
$\left| \begin{matrix} \vec{a} \end{matrix} \right| = \sqrt[2]{(4)^2+(-3)^2+(5)^2} =7.071$

Entonces el vector $\vec{a}$ normalizado es:

$\hat{a}$ = $(\frac{-4}{7.071}\hat{i}, \frac{-3}{7.071}\hat{j}, \frac{5}{7.071}\hat{k})$

$\hat{a}$ =(0.5657 $\hat{i}$ ,-0.4243 $\hat{j}$ ,0.7071 $\hat{k}$ )

$\left| \begin{matrix} \vec{a} \end{matrix} \right|$ = $\sqrt[2]{(a_x)^2+(a_y)^2}$ = $\sqrt[2]{(-3)^2+(5)^2} =5.83$

En el gráfica superior vemos que $a_x$ es el cateto adyacente al ángulo β, por lo que usando la función cos(β), que es igual al cateto adyasente entre la hipotenusa, y despejando $a_x$ se obtiene la componente del vector sobre el eje "x".

$cos( \beta)$ = $\frac{a_x}{\left| \begin{matrix} \vec{a} \end{matrix} \right| }$

$a_x$ =- $\left| \begin{matrix} \vec{a} \end{matrix} \right|$ $cos(\beta)$

De igual manera obtiene la componente $a_y$ del vector, pero ahora usando la función seno $\beta$ que relaciona al catero opuesto entre la hipotenusa.

$sen( \beta)$ = $\frac{a_y}{\left| \begin{matrix} \vec{a} \end{matrix} \right| }$

$a_y$ = $\left| \begin{matrix} \vec{a} \end{matrix} \right|$ $sen(\beta)$ .

$F_x$ = $\left| \begin{matrix} 6 \end{matrix} \right|$ $cos(28°)$ =5.3 N

$F_y$ =- $\left| \begin{matrix} 6 \end{matrix} \right|$ $sen(28°)$ =-2.83 N

Componente $y$ del vector

$b_y= \left| \begin{matrix} \vec{b} \end{matrix} \right| cos( \beta)$

Proyección del vector sobre el plano $xz$

$m= \left| \begin{matrix} \vec{b} \end{matrix} \right| sen( \beta)$

Componente $x$ del vector

$b_x=mcos( \alpha) = \left| \begin{matrix} \vec{b} \end{matrix} \right| sen( \beta )cos( \alpha)$

Componente $z$ del vector

$b_z= msen( \alpha )=\left| \begin{matrix} \vec{b} \end{matrix} \right| sen(\beta )sen(\alpha )$

$F_y= \left| \begin{matrix} 40 \end{matrix} \right| cos( 30°) = 34.64 N$

$F_x=\left| \begin{matrix} 40 \end{matrix} \right| sen( 30° )cos( 50° ) = 12.86 N$

$F_z=\left| \begin{matrix} 40 \end{matrix} \right| sen( 30° )sen( 50° ) = 15.32 N$

Su pongamos que se tienen dos vectores $\vec{\text{a}}$ y $\vec{\text{b}}$ , cuyas componentes son $(\text{a}_x,\text{a}_y,\text{a}_z)$ y $(\text{b}_x,\text{b}_y,\text{b}_z)$ respectivamente.Entonces la suma vectorial se realiza de la siguiente manera:

$\vec{\text{a}}$ + $\vec{\text{b}}$ = ( $\text{a}_x +\text{b}_x, \text{ a}_y +\text{b}_y, \text{a}_z +\text{b}_z$ )

\begin{align}\overset{\rightarrow}{\text{a}} + \left( \overset{\rightarrow}{\text{b}} +
\overset{\rightarrow}{\text{c}} \right) = \left(
\overset{\rightarrow}{\text{a}} + \overset{\rightarrow}{\text{b}} \right) +
\overset{\rightarrow}{\text{c}}\end{align}

\begin{align}\overset{\rightarrow}{\text{a}} + \overset{\rightarrow}{\text{b}} =
\overset{\rightarrow}{\text{b}} + \overset{\rightarrow}{\text{a}}\end{align}

Para cualquier vector $\vec{\text{a}}$ existe un vector - $\vec{\text{a}}$ que sumados dan como resultado el vector nulo, este vector se denomina vector opuesto y es único para el vector $\vec{\text{a}}$ .

\begin{align}\overset{\rightarrow}{\text{a}} + \left( – \overset{\rightarrow}{\text{a}}
\right) = \overset{\rightarrow}{\text{0}}\end{align}

\begin{align}\overset{\rightarrow}{\text{a}} + \overset{\rightarrow}{\text{0}} =
\overset{\rightarrow}{\text{a}}\end{align}

El producto punto es otra de las operaciones que se realiza entre vectores y da como resultado una cantidad escalar, se representa mediante un punto entre los vectores involucrados, $\vec{a} \bullet \vec{b}$ . Su interpretación gráfica es la proyección que tiene un vector sobre otro.

$\vec{a}$ $\bullet$ $\vec{b}$ = $a_x$ $b_x$ + $a_y$ $b_y$ + $a_z$ $b_z$ .

Si las componentes del vector $\vec{a}$ son (5 $\hat{i}$ , -4 $\hat{j}$ , 1 $\hat{k}$ ) y las del vector $\vec{b}$ son (-1 $\hat{i}$ , 3 $\hat{j}$ , 4 $\hat{k}$ ) de termine, $\vec{a}$ $\bullet$ $\vec{b}$ .

| $\vec{a}$ $\bullet$ $\vec{b}$ | = |(5)(-1)+(-4)(3)+(1)(4)|=|-13|=13

$\vec{a}$ $\bullet$ $\vec{b}$ = $\vec{b}$ $\bullet$ $\vec{a}$

k(( $\vec{a}$ $\bullet$ $\vec{b}$ )=( $k\vec{a}$ ) $\bullet$ $\vec{b}$

$\vec{c}$ $\bullet$ ( $\vec{a}$ + $\vec{b}$ )= $\vec{c}$ $\bullet$ $\vec{a}$ + $\vec{c}$ $\bullet$ $\vec{b}$

$\vec{c}$ $\bullet$ ( $\vec{a}$ + $\vec{b}$ )= $\vec{c}$ $\bullet$ $\vec{a}$ + $\vec{c}$ $\bullet$ $\vec{b}$

La magnitud del vector $\vec{c}$ se obtiene haciendo la siguiente operación:

$\vec{c}$ =| $\vec{a}$ | | $\vec{b}$ | sen( $\beta$ )

La dirección y sentido del vector $\vec{c}$ deberá obtenerse con la regla de la mano derecha

c=axb= $\left| \begin{matrix} \hat{i} & \hat{j} & \hat{k} \\ a_x & a_y & \ a_z \\ b_x & b_y & b_z\end{matrix} \right|$ = $[ (a_y b_z)- (a_z b_y) ] \hat{i}- [ (a_x b_z)- (a_z b_x) ] \hat{j}+ [ (a_x b_y)- (a_y b_x) ] \hat{k}$