libro digital
1. Vectores
1.4. Vectores unitarios y normalización de un vector
Vector unitario
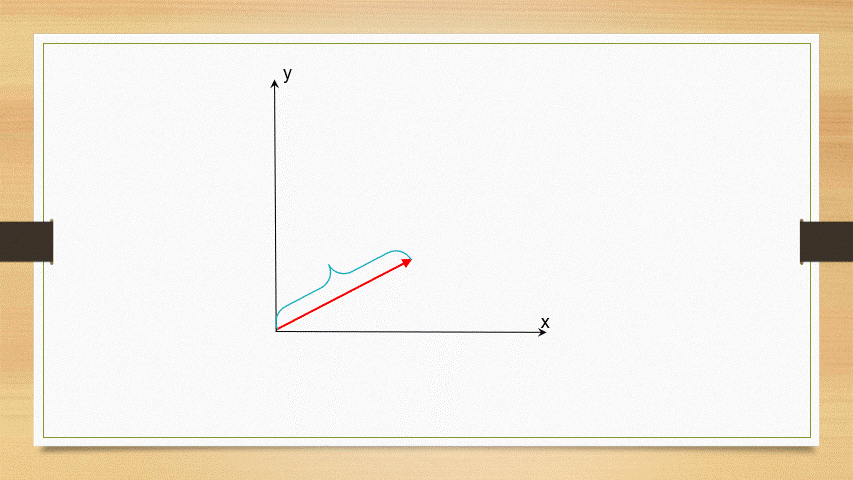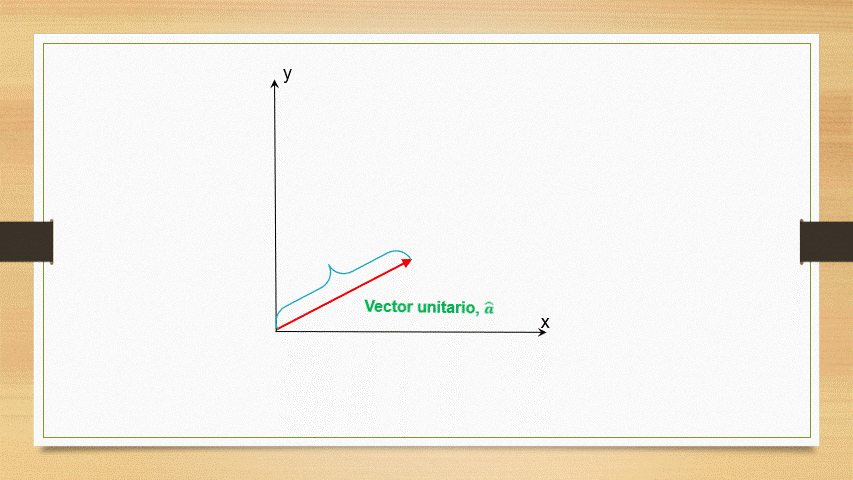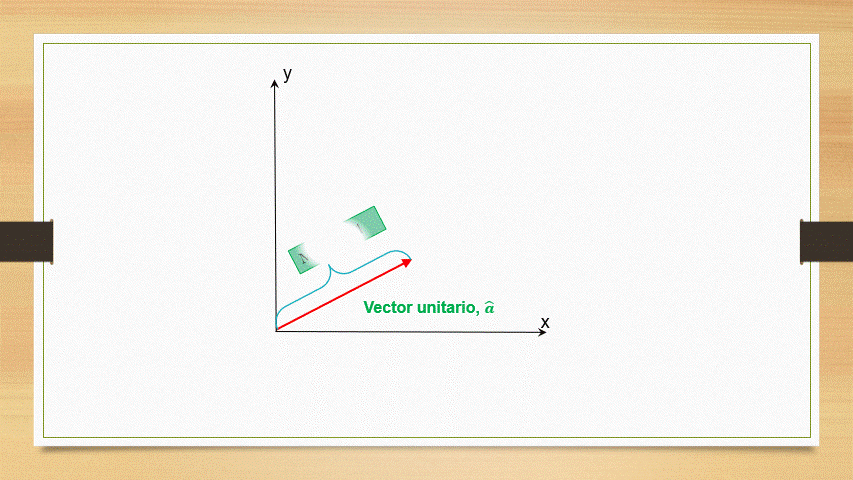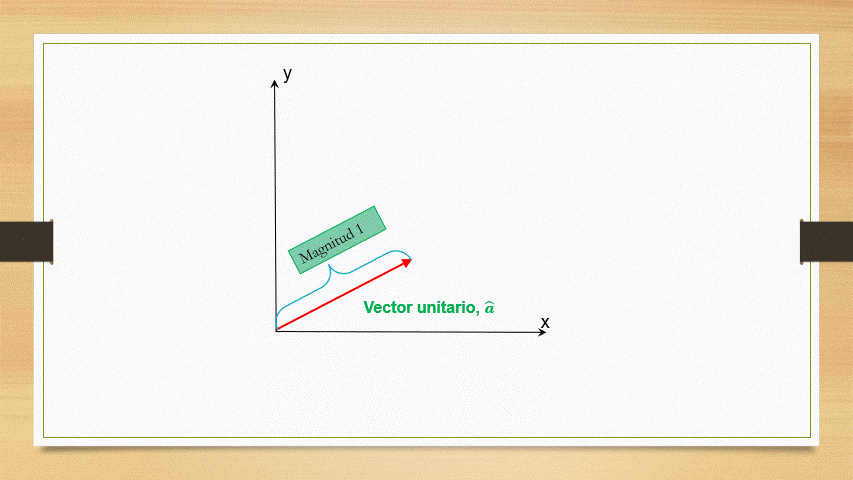
Los vectores unitarios son aquellos cuya magnitud tiene como valor al unidad. En general para representarlo se utiliza una letra la cual tiene encima de ella un símbolo circunflejo, por ejemplo, 
En física se conocen 3 vectores unitarios que tiene respectivamente la dirección del eje x,
 =(1,0,0), el eje y,
=(1,0,0), el eje y,  =(0,1,0) y el eje z,
=(0,1,0) y el eje z,  =(0,0,1). Además estos vectores son ortogonales entre si por esas dos características son llamados vectores ortonormales.
=(0,0,1). Además estos vectores son ortogonales entre si por esas dos características son llamados vectores ortonormales.
Normalización de un vector
Cuando hablamos de normalizar un vector nos referimos a que a partir de este vamos a obtener un vector unitario cuya dirección y sentido serán los mismos que la del vector original. Para llevar a cabo la normalización es necesario conocer la magnitud del vector y sus componentes. Por ejemplo, supongamos que tenemos un vector de magnitud  , y cuyas componentes se conocen y son
, y cuyas componentes se conocen y son  . Entonces, el vector unitario asociado a
. Entonces, el vector unitario asociado a  será:
será:
 =
= .
.
Ejemplo:
Normalice el vector  cuyas componentes son (4
cuyas componentes son (4 ,-3
,-3 ,5
,5 ) .
) .
- Determinar la magnitud del vector a través de sus componentes
- Dividir cada componente entre la magnitud que se determino en el paso previo.
Entonces el vector normalizado es:
 =
=
 =(0.5657
=(0.5657 ,-0.4243
,-0.4243 ,0.7071
,0.7071 )
)
Si determinamos la magnitud de este vector veremos que es de aproximadamente 1.